作者: 发布时间:2020-02-27 14:58:50 来源:复旦发展研究院+收藏本文
复旦大学社会发展与公共政策学院教授
自2019年12月8日新冠病毒爆发以来,疾病的播散速度正在加快。从12月8日的第1个病例到超过第500个病例,期间大约经历40多天的时间,即确认感染患者在1月22日达到571例,而确认感染患者达到第2个500例却只用了2天的时间(白岩松、冯子健,2020)。在1月27日晚6点多,累计报告确诊病例是2800多例,到1月27日24点则为4515例,也就是说从第3个1000例到第3个1000和第4个1000例可能分别只需1天和半天的时间。当然,截至2月5日,最新的数据已经达到2.8万例了,可见,疫情正处于加速发展阶段。所有专家、学者和政策决策者都非常关心感染人群数量会在何时以及何种规模之处达到峰值,从而转入快速下降和良性控制的轨道。
应该说,所有人都非常关心疫情的拐点到底何时到来。民众期盼早点结束受限的生活,回到工作岗位、学校或回归出门旅游、购物、聚会等生活常态;各行各业的产业组织需要根据疫情进行生产和投资决策;政府需要依据疫情发展的趋势情形来判断控制政策是要收紧加码,还是放松甚至结束。能否对疫情进行准确的预测或估计对于政府的政策决策质量至关重要。非典疫情时期,王岐山作为代市长在接受记者采访时就明确表示拒绝预测,对当时的北京非典疫情会在何时,特别是10天之后是否会迎来转折点这一问题,他说不会做这样的预期,但是他强调会对疫情发展的未来趋势做出判断。这位政治家的话语非常机智敏锐地把握和洞悉了政策决策对于疫情变化趋势预测的高度依赖性。
那么如何模拟和预测新冠病毒肺炎这类疫情的发展趋势呢?克马克和麦肯德里克(Kermack and McKendrick,1927)开发的经典传染病学模型运用了数学模型简化各类传染病传播的复杂过程,其核心变量包括感染目标人群和感染模式,其中,目标人群涉及易感者、感染者和康复者等,刻画感染模式的变量如感染速率、感染概率和感染率等。传染病模型近年来不仅在国际公共卫生领域被广泛运用,而且也同样被国内学者用来分析和研究非典、H1N1 甲型流感以及非洲的埃博拉病毒的传播和控制。不过,现在微观仿真技术的进步使得很多基于多主体的微观行为模拟也非常流行。
虽然已有一些初步研究也试图对该疫情运用传染病模型进行模拟和预测,但是任何模拟和预测都存在共同的局限性,即一方面,模拟系统或模型构造本身高度依赖于一系列的变量参数的假设,而这些参数假设都高度受制于实际的经济行为和条件变化的影响,更不用说大量具体的公共政策和制度对这些参数条件的影响了。而另一方面,模拟预测的模型机构中不同变量之间函数关系的设定具有强制性或任意性。如一些变量函数关系被认为的或模拟系统默认的比如正态分布或某种函数的形式,但事实上,变量之间的关系可能并不服从于这样的函数形式。可见,以上任何一点因素的微小变化都会造成模拟系统结果的显著变化(正所谓“失之毫厘,谬以千里”)。
正由于模拟预测系统自身的局限性以及真实世界的复杂性,尽管很多学者都试图对当前疫情的走向进行模拟和预测,但事实上很少有人愿意公布或透露其预测结果,毕竟能够准确预测何时走向峰值是非常困难的,模拟者还缺乏大量的关于疫情的具体信息和对病毒传播的路径及其机制特点的深入了解。
特别是考虑到很多从事传染病模拟和预测的专家,其研究领域属于公共卫生或医学情报研究等,传染病模型的技术性由于没有充分考虑到当前的中央及各级地方政府所开展的“联防联控”政策措施,以及新媒体、新技术条件下,公众个体自我健康管理意识的提高对疫情传播和扩散的控制效果。当然,除此之外,很多具体的技术性因素也会影响疫情或政策干预效果模拟的准确性,如数据的准确性、统计口径问题、患者确诊的时滞或遗漏等等。因此,仅仅基于技术性传染病模型的模拟来预测和评估当前的新冠病毒疫情的控制模式及其政策干预的效果,也一定会存在明显不足。
不过,虽然准确预测新冠病毒疫情走向很困难,但是,学者仍然热衷于对疫情趋势的模拟和预测分析,即使不够准确的预测结果会让人失望,但模拟和预测分析本身为研究者对于问题性质以及不同政策干预效果的比较,包括趋势的判断提供支持和帮助。流行病学家做的大量关于疾病扩散的趋势判断从形态上在大多数情形下是正确的,尽管具体趋势变化的转折时间节点难以准确预测,但是,趋势的把握和判断降低了人们对于未来情形判断或估计的不确定性。同时,对政策干预不同情境分析的模拟和预测显然会有助于研究者判断疫情走势对不同政策干预工具的敏感性,以确定其优劣或效果。
正是基于疫情预测的价值,尤其是对政策决策的支撑作用,我的同事朱勤教授和我在疫情暴发之后,就一直试图引入政策系统动力学的模型,对技术性传染病模型进行改良和修正,以加入更多的经济社会与政策干预的变量,从而改进和提升模型的解释力和预测能力。认识到传染病干预政策系统的动态性,每个政策系统内的变量随着时间的推移一般都是可变的。当然,研究的最终目的是寻找政策的最佳干预点。政策干预是选择短期效果好的还是长期效果好的,如何把干预的正向作用和副作用识别出来,通过什么控制方式选择那些与政策目标最接近的干预点或最有效的干预点,这还需要对负面的反馈循环机制进行控制(赵德余,2019)。当然,新冠病毒肺炎干预的政策目标是控制和降低被感染人群规模以及恢复被感染者的健康。具体而言,政策干预的子目标包括控制新冠病毒肺炎的感染源或患者与其他健康人群的接触率、控制易感人群的规模、提高疑似患者的确诊率、降低确诊患者的死亡率以及提高确诊患者的康复率等目标。
当然,我们还必须承认,有关疫情模拟和预测的各种困难和影响因素也同样困扰着我们的预测研究,数据的准确和有限性,以及我们模型结构相对于复杂的新冠病毒传染模式而言显然过于简单。两周以来,对该模型的结构和参数已经做了三次调整,每一次模拟和预测的结果都会发生显著的变化。坦白地说,我们的模型内生的每个变量参数如果按照干预政策可能产生的任何影响稍作调整的话,各种情景分析都会显示出很大的变化。因此,我把我们一周前完成的预测结果显示在这里,仅供批评(考虑到最近一周疫情形势变化很大,我们的原始模型结构以及参数系统还应当做进一步修正和完善)。
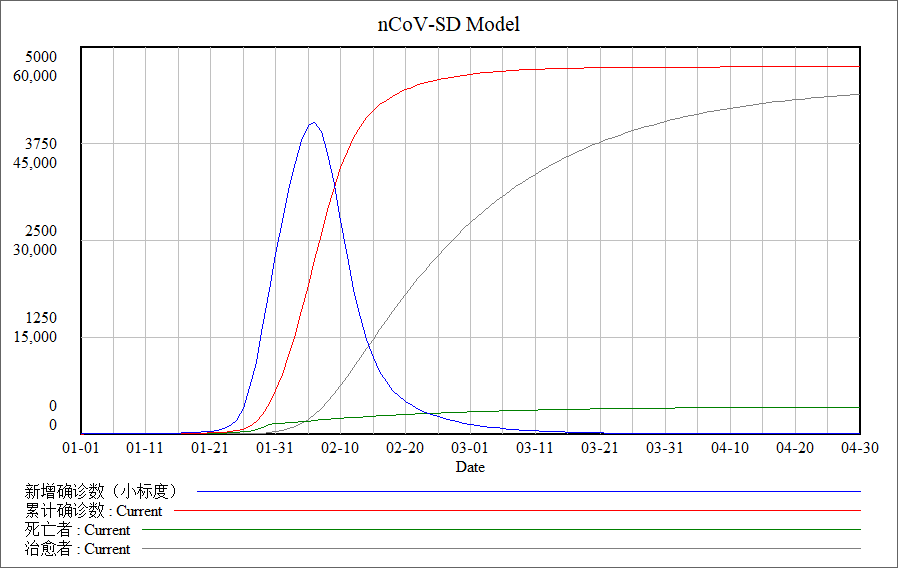
图1 新冠病毒肺炎疫情传播走势的系统动力学模拟结果
扩散型增长模型在系统结构行为学上的核心特征是其变动曲线是以正效率不断加速上升的(如图1所示),这可以通过直观的陡峭的曲线来让决策者产生深刻印象。虽然,技术性的传染病扩散模式对疾病传播的真实的复杂过程进行了高度简化,很多政策干预变量的作用没有包含在模型中,但是,政策干预的最终目的是十分清晰和明确的,即让系统行为曲线的加速上升趋势得以遏制、停止或掉头,以减弱其影响力与传播的速度(赵德余,2019)。如图1所示,在现有的模拟系统中,根据我们的模型结构和参数设计,该系统显示了在2月8-9日前后,新增确诊病例可能会在达到一个峰值之后出现稳定的下降趋势(新增确诊值最高可能在4000例左右),累计确诊数可能会于3月初达到一个高值(58000例左右),当然,这是考虑到一个未来比较高的治愈出院速率了。无论如何,我们必须承认,这里的结果仅仅是我们诸多模拟预测中一个基于大量假设条件下的可能状态的演示,尤其是2月8日之后,大规模的春节返程人员流动带来的疫情扩散风险是很难估量的,这里给出的模拟与预测很难直接或实际的参考价值。模拟结果的演示只是在此特殊的时期里,试图分享我们对于政策科学的模拟和预测能力的检讨,以及对于在当前复杂的疫情形式下,为何我们社会科学家不能准确预测疫情,甚至不愿意公开预测结果的反思。
总之,现有的各种技术性模型,包括我们自己开发的模型,都无法充分考虑到政策干预和社会的复杂因素,而目前大家都关心超大规模社会下,政策干预对于疫情控制的效果问题,尽管我们对于系统动力学模型的建构和完善做了各种尝试,但结果仍不能令人满意,这意味着,我们整个社会科学界在政策实验和模拟方法、技术的研究上还需付出很大的努力。
注:本文写作于2020年2月6日,仅代表作者本人观点。